¿cómo buscar?

Anécdotas
Curiosidades
Elementos
Experimentos
La Pregunta
Archivo
Textos
Clásicos
En la Cocina
Citas
Chistes
Exámenes
Libros
Enlaces

En el primer caso en que hemos de hacer fuerza hacia arriba para poder quitar la chapa, se necesitará hacer menos fuerza, ya que según la ley de la palanca (Ff=Rr; siendo F la fuerza que hace el dedo y R la resistencia, es decir, la fuerza que hace la chapa al oponerse a abrirse, y siendo f la distancia de la fuerza F hasta el punto de apoyo y r la distancia de la resistencia hasta el punto de apoyo), si despejamos la F nos queda: F=Rr/f, de tal manera que en el primer caso en el cual hacemos la fuerza hacia arriba, la distancia entre donde el dedo ha de aplicar la fuerza y el punto de apoyo es mayor que en el segundo caso, y como la distancia que va desde la fuerza hasta el punto de apoyo se encuentra dividiendo, el valor del primer caso será mas pequeño y por tanto conllevará menos fuerza.
 

Es un problema de palancas. La fórmula general para palancas es:

"El producto de la fuerza por su brazo es igual al producto de la
resistencia por el suyo"

                                    F x D = R x d      , donde

F= fuerza para abrir la botella (el dedo)
D= distancia del punto de fuerza al punto de apoyo
R= resistencia de la chapa a abrirse
d= distancia del punto de resistencia al punto de apoyo

En las dos imágenes se mantiene constantes R y d, es decir la
resistencia y su brazo de palanca, aun siendo palancas de distinto tipo.
El brazo D en la imagen de la izquierda (Palanca de 2º orden) es mayor
que la de la derecha (Palanca de 1º orden) . Con una sencilla operación
se comprueba que para mantenerse la igualdad F debe ser menor en la
imagen de la izquierda. Por tanto se hará menos fuerza en la botella de
la izquierda

Joaquín

Está claro que según la ley de la palanca (momento de una fuerza) se realizará menos fuerza en la situación en la que se aplique a mayor distancia del punto de giro.
Es decir el primer dibujo (izquierda).

Pero ¿Cuánto pesa el abrebotellas? En este caso la fuerza va dirigida hacía arriba y por tanto será la fuerza para deformar la chapa sumada a la fuerza para elevar el peso del abrebotellas (Realmente no son fuerzas, son momentos). En el segundo gráfico (el de la derecha) el peso del abrebotellas ayuda para aplicar el momento de giro que deformará la chapa por lo que el momento que apliquemos nosotros  será menor y por ello la fuerza.

En cualquier caso estimo que el momento para deformar la chapa pondera más que el momento del peso del abrebotellas y por tanto en el primer caso se aplica menos fuerza. Sin embargo yo por comodidad seguiré utilizando el segundo gráfico.
Joaquín.
 

En el caso que utilizamos la palanca de 2do género (con el mango del
abridor hacia abajo), haremos menos fuerza para abrir la botella, porque la
relación de distancias o palancas es favorable.

Explicación
si llamamos:
P :  la fuerza que hace nuestro dedo
R : la fuerza necesaria a aplicar en la tapa para abrirla
L : la longitud del abridor
a : la distancia entre el punto de apoyo y la fuerza R
b : la diferencia entre L y a. ( b = L - a )


PRIMER CASO: palanca de 2do género

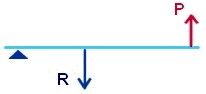	<------a------><--------  b  ---------> <----------------  L  ------------------->

 en este caso será P x L = R x a, entonces P = ( R x a ) / L


SEGUNDO CASO: palanca de 1er género

en este caso será P' x b = R x a, entonces P' = ( R x a ) / b

si comparamos las ecuaciones, vemos que "R" y "a" están en ambas, en el
primer caso están divididas por "L" que es mayor que "b", por lo tanto la
fuerza P es menor en este caso

o continuando con las ecuaciones

P' / P = ( R x a / b ) / ( R x a / L )
entonces
P' / P = L / b
pero sabemos que
L > b
entonces
P' / P > 1
entonces
P' > P o lo que es igual a que en el segundo caso, haremos más fuerza que
en el primero